这是2018CVPR的一篇论文(原论文地址:https://arxiv.org/abs/1711.06077), 论文主要说明感知质量和图像失真程度并不是完全对应的。基于深度网络的特征失真可能更好的表示图像感知质量的好坏,而使用GAN网络可以获得具有较好感知质量效果的图像。失真-感知之间存在一个可以实现的区域,在这个可以实现的区域里失真程度和感知质量并不是完全的相关,也就是失真较大时感知质量也可能比较好,论文给出的图如下所示:
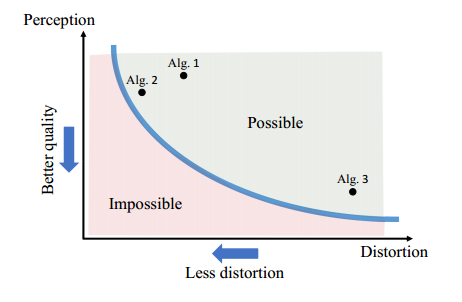
失真和感知质量
失真用来衡量给定图像和参考图像之间的差异程度。最常见的失真是MSE,但是与图像之间的语义相似性比较差。其他衡量失真的标准包括SSIM、MS-SSIM等,最近基于神经网络的距离误差可以捕获更多的语义信息,从而获得高质量的重建。
感知质量是使图像看起来和自然图像更像而不考虑其与参考图像之间的相似性。目前主要的评价方法包括基于人类评价的质量评估方法,无参评价方法(如KL散度)和基于GAN网络的评价方法,这些方法基本都是利用统计学的知识进行评价。
建立问题的公式
实际上自然图像可以看做是自然图像pX的自然分布的一个实现,可以把失真后的图像y看成是给定原图像x在条件分布pY|X下产生的结果,失真后还原的图像x’可以看成y在条件分布pX|Y产生的结果。失真的公式可以表示如下:
感知质量指标的表达式如下(值越低越好):
论文的目标是建立上面两个公式的平衡,首先说明为什么减少(1)不能必然导致较低的(2)。
这里论文主要使用了两种失真方式去衡量图像失真。一种是均方误差失真(MMSE),另外一种是0-1失真(MAP)。x的原始分布是{-1,0,1}时,前者导致产生的结果是连续的,后者导致结果只有{-1,1}。换言之就是失真评估的方法会使图像掉落自然分布的”流型“,从而使分布与原始图像不同。具体见下图所示:
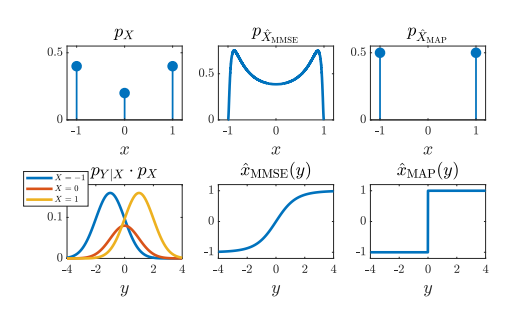
感知-失真平衡
从上面可以看出低失真不一定能带来较好的感知质量,如何在给定失真的情况下得到最好的感知质量需要研究。信号恢复任务的感知-平衡函数由下式给出:
论文给了一个感知-失真平衡定理,即如果(2)中第二个参数是凸的,那么感知-失真平衡函数是:(1)不单调增的。(2)凸的。
该定理不需要对失真度量进行假设,也就是对任意的感知-失真都存在这样的度量。虽然这并不意味着所有的失真都存在相同的感知-失真函数。P(D)的凸特性说明其在低失真和高感知的情况下存在非常严重的平衡。例如低失真情况下略微的失真改善会导致感知质量大幅度下降,同理,高感知情况下略微的感知改善会导致失真大量增加。
然后讨论了感知-失真和速率失真理论的联系。信号的速率失真函数和互信息密切相关。当然速率失真和要讨论的情况有一些不同,这里可参考论文不再赘述。
通过GAN进行平衡
可以通过GAN来设计接近感知-失真平衡曲线的估计器。具体可以通过修改损失函数得到,如下所示:
第一项表示失真,第二项的生成器学习d(pX,pX’),所以(4)式接近于学习目标:
这里最小化(5)可以等效为最小化(3),变化的$\lambda$产生变化的D,从而产生感知-失真函数的估计量。可以使用这种方法去获得感知-失真平衡,通过将$\lambda$设定为[0,0.3]之间,改变参数可得到曲线,如下图所示:
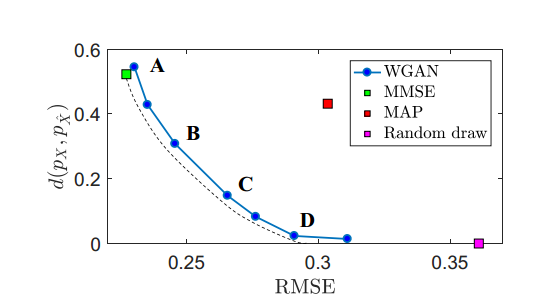
同样可以看出,失真函数使用MMSE比使用MAP在产生相同失真情况下,感知质量更好,同时也比随机抽取的失真要小。
实用的评估算法
定义:如果算法A在失真和感知质量上优于算法B,则称算法A支配算法B。(注意:如果无法同时在失真和感知质量上有较好的效果,那么算法A和算法B无法一方支配另一方,认为它们具有同样好的效果)。
定义:如果一个算法不被一组算法中的其他算法支配,那么这个算法被认为是可以接受的。
论文这里说明失真一般通过全参考(FR)方式来度量,包括(RMSE/SSIM/MS-SSIM/IFC/VIF/VGG2.2)等。为了评价图像的感知质量,这里采用了无参考(NR)指标。这里对16种SR算法从FR和NR进行评估,结果如下图所示:
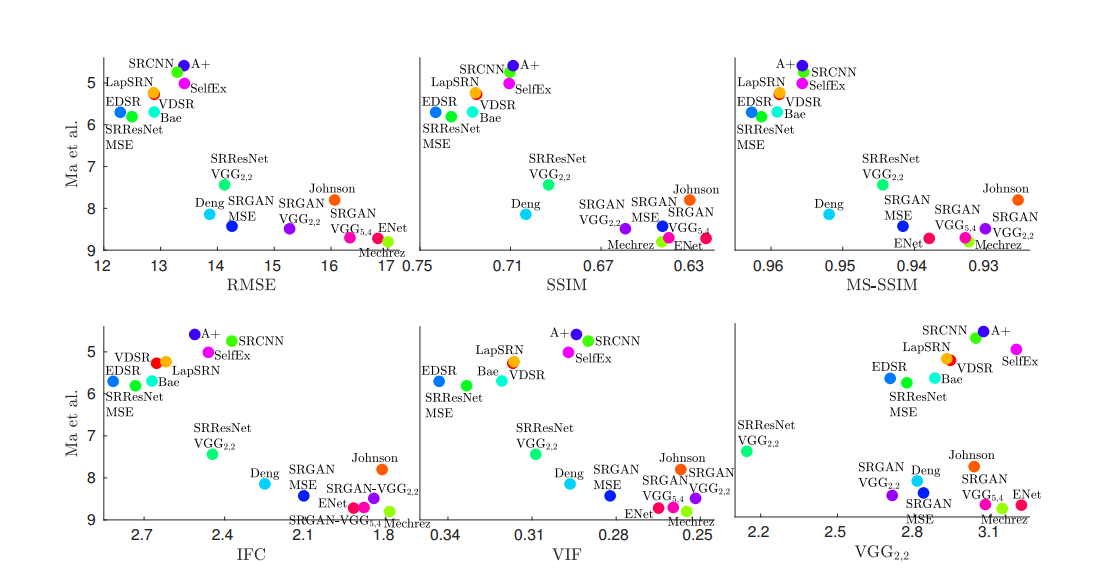
上图各部分都有共同的特点:(1)左下方是空白的,这反映感知-失真平面中的不可到达区域。(2)NR和FR指标是负相关的,这反映感知-失真的平衡。虽然IFC和VIF相比于SSIM和MSE可以更好的捕获视觉质量,但是也存在这种平衡。VGG2.2的平衡现象比MSE略弱,说明其是一个相对更感知评价指标。从上图中还可以看出,从左到右失真增加,但是感知质量是提高的。
当远离不可到达区域时,FR和感知质量可以达到正相关,接近不可达达区域时却不符合,FR此时不能用来衡量图像感知质量,而NR可以用来表示感知质量好坏。因此在评估时需要对FR和NR统一进行评估,兼顾失真和感知质量。具体如下图所示:
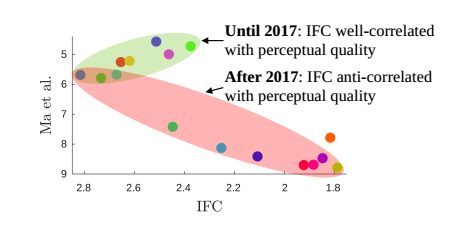
在2017年之前,IFC指标可以很好的匹配感知质量,2017年以后就开始反相关。这篇论文说明了失真和感知质量之间存在矛盾,可以使用一对NR和FR指标进行评价比较。