这是去年计算成像学领域的一篇论文(链接:https://ieeexplore.ieee.org/document/7797130/ ),重在讨论如何损失函数对图像恢复的影响。在目前的图像恢复任务中主要使用的还是L2损失函数,L2损失的好处有很多,例如可以直接提高PSNR等指标。但是L2指标与人类感知的图像质量相关性较差,例如其假设噪声与图像的局部区域无关。在有些情况下,L1损失函数获得的图像质量会更好。这里论文调研了L1损失,SSIM和MS-SSIM,并将L1损失函数和MS-SSIM结合起来构建新的损失函数。但是目前为止,基于SSIM的指标还没有应用到损失函数中。
L1损失函数
同L2损失函数相比,L1损失函数不会过度惩罚两张图的差异,因此它具有不同的收敛属性。L1损失函数可以表示为:
其微分形式表示如下:
在实验中,L1函数在许多问题上的表现要比L2函数好。
SSIM损失函数
SSIM结构性指标定义如下:
SSIM的值一般是越大越好的,所以这里损失函数设定为:
但是SSIM计算时是和周围像素比较,上式显然没有考虑像素在边界的情况,所以损失函数可以改写为:
此时后面的p’代表中心点的像素。
最后,SSIM的微分形式为:
其中$\begin{eqnarray} \frac{\partial l(\tilde{p})}{\partial x(q)} = 2\cdot G{\sigma _G}(q-\tilde{p}) \cdot \left(\frac{\mu _y-\mu _x\cdot l(\tilde{p})}{\mu _x^2+\mu _y^2+C_1} \right) \end{eqnarray}$,$\begin{eqnarray} \frac{\partial cs(\tilde{p})}{\partial x(q)} &=& \frac{2}{\sigma _x^2+\sigma _y^2+C_2} \cdot G{\sigma _G} (q-\tilde{p}) \cdot \big [ \left(y(q) - \mu _y\right) \nonumber\ & & - \, cs(\tilde{p}) \cdot \left(x(q) - \mu _x\right) \big ], \end{eqnarray}$
MS-SSIM
$\sigma_{G}$的大小影响图像的效果,较小会失去保持局部的能力,较大会保持边缘噪声,因此使用多尺度的SSIM即MS-SSIM,定义如下:
损失函数类似SSIM,可以表示为
微分形式为:
MS-SSIM和L1结合
MS-SSIM和SSIM对亮度和色彩变化可能会更迟钝,但是可以较好的保持高频信息,L1则可以较好的保持颜色亮度特征,因此可以将它们结合起来,综合损失函数如下:
这里$\alpha$设定为0.84。
结果
图像去噪,超分辨和图像去伪影的对比表分别如下所示,可以看出混合后的效果最好:

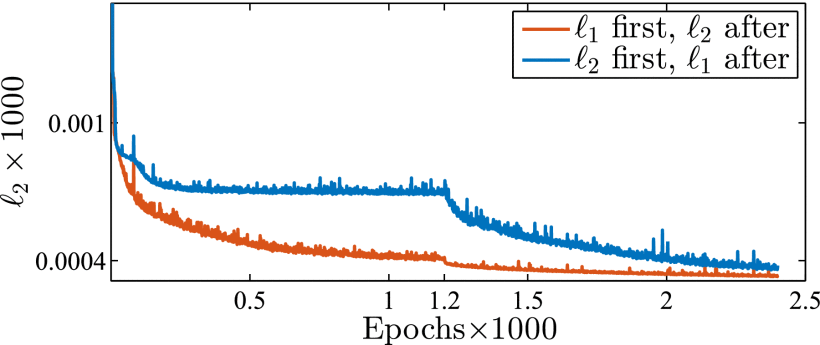
论文还对损失函数的收敛性进行研究,说明L1收敛性比L2更好,如下图所示,在切换损失函数前,L1下降更快,说明L2之前可能陷入局部最小。