阅读论文《SID NISM:A Self-supervised Low-light Image Enhancement Framework》

   2020挂在arxiv的一篇论文，自监督低光照增强

现有方法的问题

1.需要成对的数据
2.传统的基于Retinex的方法会产生不好的artifacts

论文提出的点

1.对于输入图像使用Retinex进行分解，使用其直方图增强的结果作为辅助，最终分解成光照无关的反射图，有结构信息的光照图和与反射图相关的噪声图。
2.对于光照图使用非线性变换增强NISM，从而在增强整张图的情况下保留对比度。

论文的方法

如下图所示：

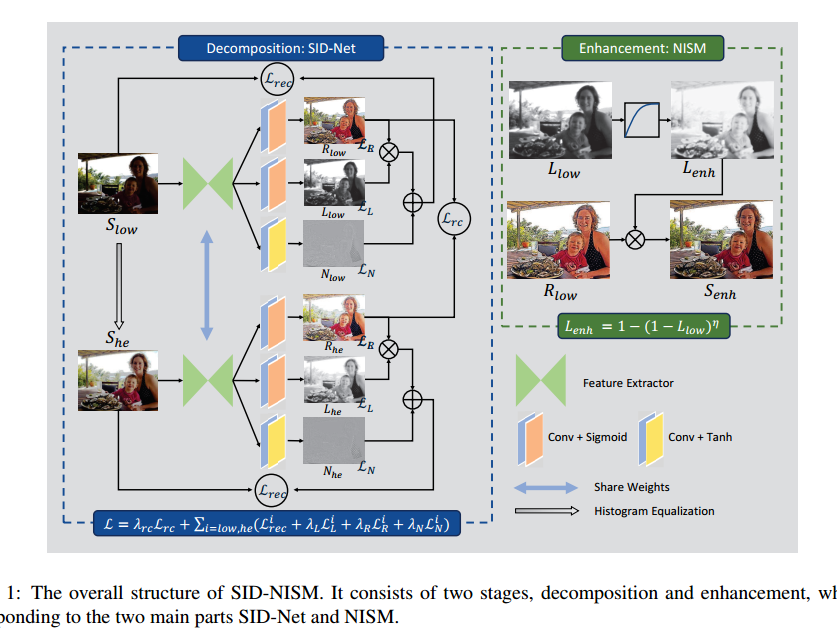
自监督分解网络SID-Net

1.这里加入直方图均衡化的结果作为中间的辅助变量也用来分解，而并不是使用GT，个人认为是为了增强分解时的鲁棒性。
2.损失函数为$L = \lambda{rc}L{rc}+\Sigma{i=low,he}(L^i{rec}+\lambda{L}L^i{L}+\lambda{R}L^i{R}+\lambda{N}L^i{N})$,其中第一项约束直方图增强后结果he和输入I，后面对he和I分别对光照图反射图和噪声图进行约束，以及重建损失。 3.重建损失函数为$L{rec}=||R\cdot L+N-S||_1$4.反射图一致损失为$L{rc} = ||R{low}-R{he}||1$5.光照图损失函数包括两项，前者使得光照图在平滑的同时和反射图在整体结构上保持一致，后者则类似于WLS损失，保留光照图中大的edge，抑制小的edge，其为$L_L = ||\triangledown L \cdot exp(-\alpha \triangledown R)||_1+||\triangledown L \cdot exp(-\alpha \Sigma{j=low,he} \triangledown Lj||_1$6.对于反射图，这里也包括两项，为$L_R = \frac{1}{3} \Sigma{ch = R,G,B}|| \triangledown R^{ch} - \beta \triangledown S^{ch}||_F+||R^H-S^H||_2$，其中第一项为让反射图的梯度是输入图S梯度的$\beta$倍，从而增强对比度，后者使得反射图和输入图色度一致，从而避免色偏。 7.对于噪声图，重建损失去除R和L的部分就是N，由于越暗的地方噪声越多，这里需要对噪声图N进行约束，为$L_N = ||S \cdot N||_F$

非线性变换增强NISM

1.伽马变换会导致暗区域过曝，而亮区域几乎没被改变（虽然亮区本来就不需要太大变化），导致对比度失调。
2.对于暗区域，增强的程度可以更低一点，而对于亮区域，增强的程度应当更大，从而使得最终增强的结果足够亮
3.使用NISM，则变化曲线表示为$\hat{L}=1-(1-L)^{\lambda}$，当$\lambda$值为2.2时，其和伽马变换的曲线如下所示，可以看出，和2的分析是吻合的

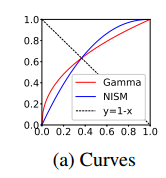
4.实际中，$\lambda$的值则是根据亮暗区域的阈值T确定的，公式为$\lambda = log(1-0.8)/(1-T)$

实验与结果

1.可以在几百个迭代内对一张图实现训练（比传统方法慢太多了吧？）
2.实验结果对比略
3.思考，论文亮点是引入直方图增强结果，其实是增强了训练的鲁棒性，引入额外数据辅助自监督是一个思路；此外，对于光照图的处理，也可以有更好的变换方式。