KKT条件的python解法

发表于 | 更新于: | 分类于 | 阅读次数: |
字数统计: 562字 | 阅读时长 ≈ 3分钟

   要求，使用拉格朗日乘子法解决下面的问题：

方法一：按照题目要求使用拉格朗日乘子法

   这个方法就是按照几个限定的约束条件来解方程，KKT条件整体如下：

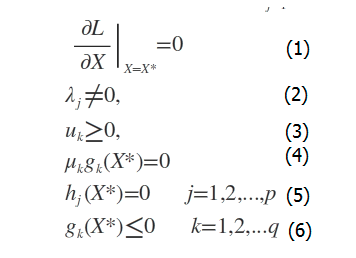
   题目的拉格朗日乘子式为L=(10−x12−x22)+λ(x1+x2)+μ(x12−x2)。
   由于python只能求解等式方程，不能求解不等式，所以这里的等式方程有（1）（4）（5）,先取出这三个式子，首先对（1）进行求导，可以获得两个两个式子，再结合（4）（5），这样就有四个方程四个未知数，可以得到理论上的解空间，这样就限定了解的范围,该部分代码如下:

1
2
3
4
5
6
7
8
9
10
from sympy import *

x1 = Symbol("x1")
x2 = Symbol("x2")
a = Symbol("a")
b = Symbol("b")
f = 10 - x1**2 - x2**2 +a*(x1 + x2) + b*(x1**2 - x2)
fx1 = diff(f,x1)
fx2 = diff(f,x2)
result = solve([fx1,fx2,(x1**2-x2)*b,x1+x2],[x1,x2,a,b])

   求出来的解可能还不是唯一的，怎么办呢，这时候用另外几个上面没有用到的条件也就是KKT里的非等式解，也就是（2）（3）（7）去获得解空间里符合条件的数值：

1
2
3
4
for i in range(len(result)):
    if result[i][3]>=0 and result[i][0]**2-result[i][1]<=0 and result[i][2]!=0:
        print(result[i])
        print("loss:",10 - result[i][0]**2 - result[i][1]**2 +result[i][2]*(result[i][1] + result[i][0]) + result[i][3]*(result[i][0]**2 - result[i][1]))

   获得最终解如下，(-1, 1, 6, 4)，(‘loss:’, 8)。

方法二：不使用拉格朗日乘子式，直接对目标函数进行优化

   这里直接使用tensorflow，对目标函数进行优化迭代，限定满足两个约束条件时才进行优化，设定初值为-0.1落在约束条件内，代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
import tensorflow as tf

x1 = tf.Variable(tf.random_normal(shape=[1],mean=-0.1,stddev=0.01))
x2 = -x1
loss = 10 - x1*x1 - x2*x2
train_op = tf.train.AdamOptimizer(1e-4).minimize(loss)


with tf.Session() as sess:
    sess.run(tf.global_variables_initializer())
    for i in range(10000):
        xs,loss_show = sess.run([x1,loss])
        if xs*xs+xs <= 0 :
            _= sess.run(train_op)
        print('step =%d,loss=%.8f,x1=%.8f'%(i,loss_show,xs))

求出解与方法一一样。

0%