在MLP上实现BP

发表于 | 更新于: | 分类于 | 阅读次数: |
字数统计: 1,094字 | 阅读时长 ≈ 6分钟

题目要求如下：

2018-12-05 12-09-17屏幕截图.png

首先定义激活函数，这里需要定义sigmoid激活函数和relu激活函数，以及它们的导数，如下所示：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
import numpy as np
import matplotlib.pyplot as plt

def sigmoid(x):
    return 1 / (1 + np.exp(-x))

def dsigmoid(y):
    return y * (1 - y)

def relu(y):
    return np.maximum(0.0,y)

def drelu(x):
    tmp = x.copy()
    tmp[tmp >= 0] = 1
    tmp[tmp < 0] = 0
    return tmp

然后还是提供数据，代码如下：

1
2
3
4
5
6
7
8
9
10
def produce_data():
    X = np.array([
    [0, 0],
    [0, 1],
    [1, 0],
    [1, 1],
     ])
    y = np.array([[0,1,1,0]])
    return X,y
X,y = produce_data()

然后就是定义神经网络的结构和训练过程，如下所示：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
class MLP(object):
    def __init__(self,hidden_num=2,limit=0.01,activation='relu',lr=0.1):
        np.random.seed(8)
        self.X, self.Y = produce_data()
        self.V = np.random.random((self.X.shape[1], hidden_num)) * 2 - 1
        self.W = np.random.random((hidden_num, 1)) * 2 - 1
        if activation == 'sigmoid':
            self.activation = sigmoid
            self.dactivation = dsigmoid
        elif activation == 'relu':
            self.activation = relu
            self.dactivation = drelu
        self.lr = lr
        self.limit = limit
    def update(self):
        L1 = self.activation(np.dot(self.X, self.V))
        L2 =  self.activation(np.dot(L1, self.W))
        L2_delta = (self.Y.T - L2) * self.dactivation(L2)
        L1_delta = L2_delta.dot(self.W.T) * self.dactivation(L1)
        W_C = self.lr * L1.T.dot(L2_delta)
        V_C = self.lr * self.X.T.dot(L1_delta)
        self.W = self.W + W_C
        self.V = self.V + V_C
        return L2

    def train(self):
        L2 = self.update()
        i = 0
        plt.figure()
        error_plot = []
        dot = []
        while(1):
            L2 = self.update()
            i+=1
            error = np.mean(np.abs(self.Y.T-L2))
            if error<self.limit:
                break
            #if i%5000==0:
             #   print('Error:', error)
            if i%50 == 0:
                error_plot.append(error)
                dot.append(i)
        plt.plot(np.array(dot),np.array(error_plot))
        plt.show()
        print("迭代了%.d次收敛"%i)
        # return L2

    def predict(self,data):
        L1 = self.activation(np.dot(data, self.V))
        L2 = self.activation(np.dot(L1, self.W))
        return L2

见上面的代码，网络设置的超参包括，隐层的神经元数目，迭代终止的阈值数，激活函数类型和学习率。这里当MLP预测的标签和真实标签之间的直小于阈值时，网络停止训练，并且打印出误差和迭代次数的曲线图，以便直观反映分类器在学习时的性能。

下面代码是画图曲线，直观反映数据各个区域被划分的情况，代码如下所示：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
def plot_decision_boundary(pred_func, X, y, title=None):


    # Set min and max values and give it some padding
    x_min, x_max = X[:, 0].min() - .5, X[:, 0].max() + .5
    y_min, y_max = X[:, 1].min() - .5, X[:, 1].max() + .5
    h = 0.01
    # Generate a grid of points with distance h between them
    xx, yy = np.meshgrid(np.arange(x_min, x_max, h), np.arange(y_min, y_max, h))
    # Predict the function value for the whole gid
    Z = pred_func(np.c_[xx.ravel(), yy.ravel()])
    Z = Z.reshape(xx.shape)
    # Plot the contour and training examples
    plt.contourf(xx, yy, Z, cmap=plt.cm.Spectral)
    for i in range(y.shape[1]):
        plt.scatter(X[i, 0], X[i, 1],c=('y' if y[0][i]>0.5 else 'k'), s=40,  cmap=plt.cm.Spectral)

    if title:
        plt.title(title)
    plt.show()

def tmp(pred):
    sign = np.vectorize(lambda x: 1 if x >= 0.5 else 0)
    ans = sign(nn.predict(pred))
    return ans

最后是输出结果，这里我们分成两个：

sigmoid激活函数输出结果

很显然，按照要求隐层的神经元数目为2，阈值设为0.01，学习率调为0.55时发现此时sigmoid收敛最快，所以测试如下：

1
2
3
4
5
nn = MLP(hidden_num=2,limit=0.01,activation='sigmoid',lr=0.55)
nn.train()
pred = nn.predict(X)
print(pred)
plot_decision_boundary(tmp, X, y, 'Neural Network')

output_15_0.png

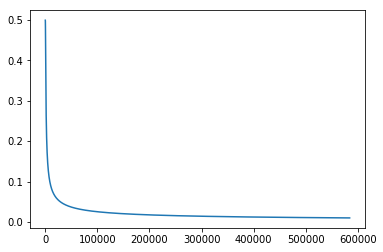
迭代了584208次收敛
[[0.0031447 ]
 [0.98899742]
 [0.98899742]
 [0.0148501 ]]

output_15_2.png

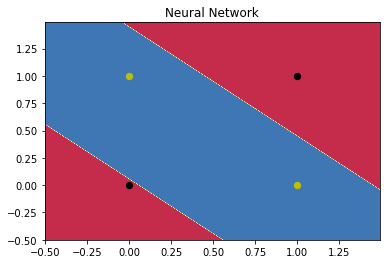
可以看出一共迭代了584208次才收敛，这无疑是一个很长的时间。

relu激活函数输出结果

这里除了学习率，其他参数设置同上，这里发现学习率为0.048时对于relu函数收敛最快，测试如下：

1
2
3
4
5
nn = MLP(hidden_num=2,limit=0.01,activation='relu',lr=0.048)
nn.train()
pred = nn.predict(X)
print(pred)
plot_decision_boundary(tmp, X, y, 'Neural Network')

output_19_0.png

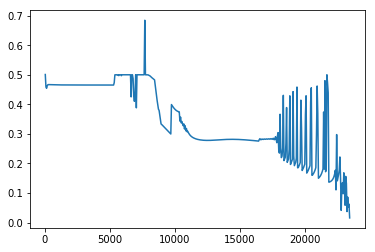
迭代了23451次收敛
[[0.        ]
 [0.98167616]
 [0.97657768]
 [0.        ]]

output_19_2.png

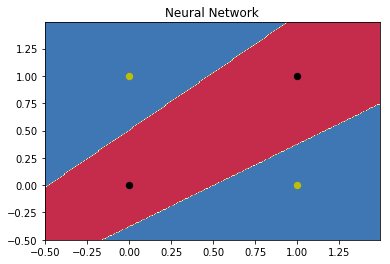
虽然相对sigmoid迭代的很快，但是收敛过程却并不稳定。

结论

1.relu函数的收敛速度比sigmoid函数快很多，所以我们一般使用relu函数做激活函数比较多。

2.sigmoid函数收敛过程比relu更加稳定，对初值的选择也不是很挑剔，其鲁棒性比较好。

0%