代码转换
原文地址为https://blog.csdn.net/dcrmg/article/details/53677739 。本人使用opencv的python版本这里面的操作进行了一下转换。代码如下所示:1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30import cv2
import numpy as np
import math
# Histogram Equalization
img1 = cv2.imread('input1.png')
dst_img1 = np.zeros(img1.shape, np.uint8)
for i in range(0,3):
dst_img1[:,:,i] = cv2.equalizeHist(img1[:,:,i])
cv2.imshow("Histogram Equalization",dst_img1)
# Laplacian
img2 = cv2.imread('input2.jpeg')
dst_img2 = np.zeros(img2.shape, np.uint8)
kernel = np.array([[0,-1,0],[0,5,0],[0,-1,0]])
cv2.filter2D(img2,cv2.CV_8UC3,kernel,dst_img2)
cv2.imshow("Laplacian Effect",dst_img2)
# Log transfer
img3 = cv2.imread('input3.jpeg')
dst_img3 = np.zeros(img3.shape, np.float32)
for i in range(0,img3.shape[0]):
for j in range(0,img3.shape[1]):
for k in range(0,3):
dst_img3[i,j,k] = math.log(1+img3[i,j,k])
cv2.normalize(dst_img3,dst_img3,0,255,cv2.NORM_MINMAX)
dst_img3 = np.uint8(dst_img3)
cv2.convertScaleAbs(dst_img3,dst_img3)
cv2.imshow("Log result",dst_img3)
cv2.waitKey(0)
自上而下依次是直方图均衡化操作,拉普拉斯增强操作和LOG变换操作,效果在原链接里已经有了,这里不再显示。
图像数据简介
首先学习的是常见的图像存储格式,如下:
CV_{bit_depth}(S|U|F)C{number_of_channels}
bit_depth:图像深度,也就是比特数,例如8位,16位,32位,64位。
(S|U|F):分别表示三种数据类型,S为signed int,即有符号整型;U为unsigned int,即无符号整型;F为float,单精度浮点型。三者只能选一种。
number_of_channels:1表示灰度图,2表示RGB图像,3表示带alpha的RGB图像也就是四通道图像。
例如:CV_8UC3,代表8位比特的无符号整型的RGB图像数据。
直方图均衡化
下面对代码里的一些图像操作进行分析,首先是直方图均衡化,通过调整图像的灰阶分布,使得在0~255灰阶上的分布更加均衡,提高了图像的对比度,达到改善图像主观视觉效果的目的。对比度较低的图像适合使用直方图均衡化方法来增强图像细节。直观原理如下图所示: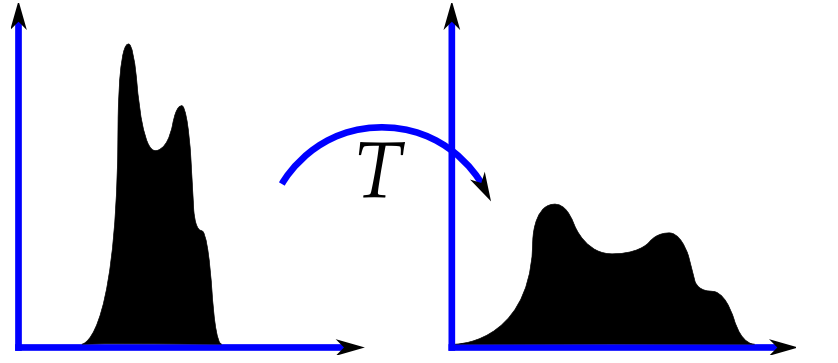
这里opencv使用的核心操作是cv2.equalizeHist,只能对一个通道进行均衡化操作,其基本定义为equalizeHist(src, dst);第一个参数为输入图像,第二个参数为输出图像。
该函数采用如下法则对输入图像进行直方图均衡化:
1:计算输入图像的直方图H。
2:直方图归一化,因此直方块和为255。
3:计算直方图积分,H’(i) = Sum(H(j)) (0<=j<=i)。
4:采用H’作为查询表:dst(x, y) = H’(src(x, y))进行图像变换。
具体的原理可以参考数字图像处理,这里不再赘述。
使用filer2D(图像卷积运算)实现拉普拉斯算子增强
使用中心为5的8邻域拉普拉斯算子与图像卷积可以达到锐化增强图像的目的,当然拉普拉斯算子的形式有很多了,其中一个如下所示:
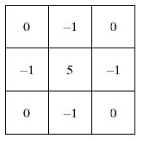
这里使用使用filer2D(图像卷积运算)来实现,即通过卷积上图所示的算子,即可实现拉普拉斯算子增强。filer2D定义如下:1
C++:void filter2D(InputArraysrc, OutputArray dst, int ddepth, InputArray kernel, Point anchor=Point(-1,-1), doubledelta=0,intborderType=BORDER_DEFAULT)
主要参数就是前面五个,InputArraysrc(输入),OutputArray dst(输出),ddepth(图像深度),kernel(操作核), Point anchor(核的基准点,默认-1表示在核的中心)。该函数使用于任意线性滤波器的图像,支持就地操作。当其中心移动到图像外,函数可以根据指定的边界模式进行插值运算。函数实质上是计算kernel与图像的相关性而不是卷积。
这里图像为I(x,y),核为G(i,j),其中0<i<Mi-1和0<j<Mj-1,锚点位于相应核的(ai,aj)坐标上。
LOG变换及其他
LOG变换这里使用了log求对数操作,一般来说在python里求对数操作有三种方式,分别是math.log(x),scipy.log(x)和numpy.log(x),这里我们使用的是math.log(x)。
LOG(对数)变换可以将图像的低灰度值部分扩展,显示出低灰度部分更多的细节,将其高灰度值部分压缩,减少高灰度值部分的细节,从而达到强调图像低灰度部分的目的。变换方法:$s=clog_{v+1}(1+v*r)$,其增强低灰度部分的一个直观的体现如下图:
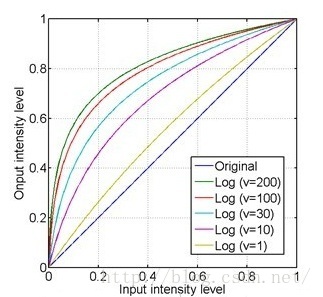
x轴的0.4大约对应了y轴的0.8,即原图上0-0.4的低灰度部分经过对数运算后扩展到0-0.8的部分,而整个0.4-1的高灰度部分被投影到只有0.8-1的区间,这样就达到了扩展和增强低灰度部分,压缩高灰度部分的值的功能。从上图还可以看到,对于不同的底数,底数越大,对低灰度部分的扩展就越强,对高灰度部分的压缩也就越强。
这部分还使用的cv2.normalize用来进行归一化,定义如下:1
void normalize(InputArray src, OutputArray dst, double alpha=1, double beta=0, int norm_type=NORM_L2, int dtype=-1, InputArray mask=noArray())
其中src:输入矩阵,dst:归一化后的矩阵,当norm_type=NORM_MINMAX时,dst的最小值为alpha,dst的最大值为beta。norm_type=NORM_INF, NORM_L1, or NORM_L2shi时,dst为src的无穷范数、1范数和2范数。例如,本例中就将图像扩展为0到255区间。
参考:
1、https://blog.csdn.net/dcrmg/article/details/53677739
2、https://blog.csdn.net/lay_zy/article/details/78399317
3、https://bbs.csdn.net/topics/390957036
4、https://blog.csdn.net/xiachong27/article/details/80520154
5、https://blog.csdn.net/u012487272/article/details/26745149