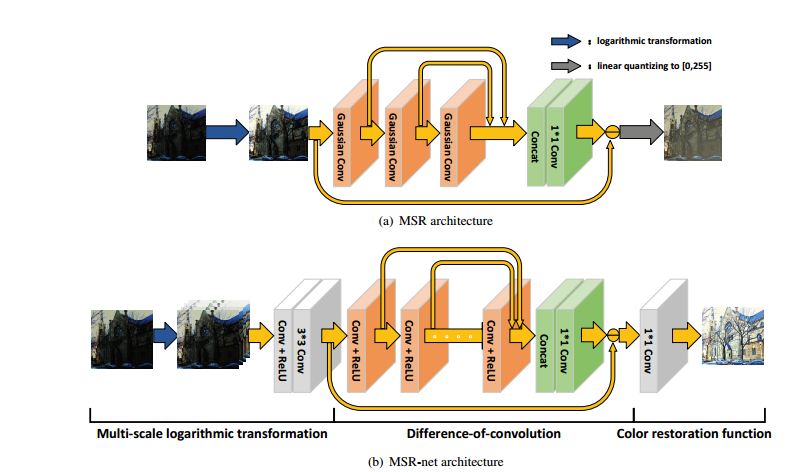
这是2017年arxiv上挂的一篇做低光照图像增强的论文,其原理是模拟mutiscale的 retinex理论使用CNN进行图像增强,基本思路是将多尺度的retinex等价于一个前向网络嵌入不同的高斯卷积核。这里基于此原理提出一个网络直接学习弱光照到强光照图像的转换。传统的MSR方法可以看做是一系列SSR方法的加权之和。MSR框架和本文提出的框架如下所示:
Retinex理论的基本公式为$I(x,y) = r(x,y) \cdot S(x,y)$,SSR使用类似于DOG的原理得到如下公式:
其中R是retinex的输出,I是第i个颜色光谱在,*表示卷积,F表示高斯环绕函数。上式其实等价于下式:
这两个式子其实并没有太大的差别在实验里,这里选择后一个式子,MSR是多个SSR输出的加权组合,表示如下:
实验证明选择n=3效果比较好,上述式子可写为:
注意到两个高斯函数的卷积仍然是一个高斯函数,方差是两者之和,所以这里可以用级联结构去表示上式,如上图(a)所示。第一个卷积核是高斯分布的,方差为$c_1^2$,后面两层分别是$c_2^2-c_1^2$和$c_3^2-c_2^2$。concat用来表示加权求和,也就是说MSR完全可以用一个有残差连接的前向传播网络来表示。
论文提出的方案将步骤分成了三步,分别是Log转换部分,卷积差部分和颜色恢复部分。在第一步,首先输入的图像被多个log转换函数进行转换,如下所示:
然后将这些M个图 concat在一起,并且通过一个卷积核卷成3通道的输入,这一步的目的是为了获得多个log转换结果的加权和,从而加速网络收敛。第二步和上面介绍的MSR的过程比较像,将该步的输入减去cooncat在一起卷积后结果获得残差,作为该步的输出。最后的图像恢复部分,这里将上面的结果通过1x1卷积进行转换,作为最后的输出。