这是2019 CVPR一篇做SR的论文,没怎么读懂,有读透的老哥来带带我orz。
论文的出发点是二阶特征attention机制去在特征维度上进行放缩,使用二阶特征统计量去实现。同样,论文提出了非局部增强模块NLRG,包括空间信息捕捉部分和局部残差attention模块LSARG去学习特征表达。目前的很多CNN方法没有充分利用原始LR图像的信息,导致相对较差的表现;大部分的CNN方法没有去发掘层内的特征关联性。所以这里利用二阶channel attention的方法去发掘特征相关性学习,同时使用非局部模块捕获空间相关性,此外通过残差连接使得低频信息可以直接通过。网络的整体结构图如下所示:
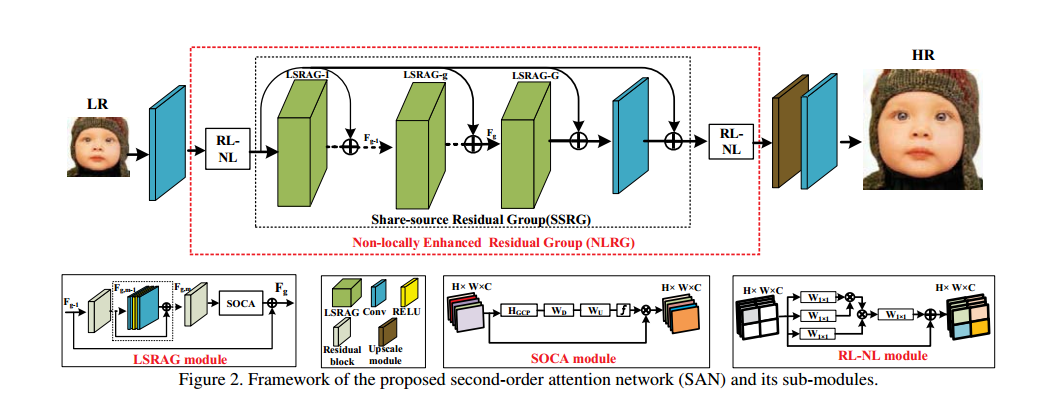
网络包括下面几个部分,浅层特征提取,非局部增强模块NLRG,上采样模块和重建模块。如上图所示,首先浅层特征提取部分获得F0,然后进入NLRG,NLRG包括RL-NL模块和若干LSRAG模块。注意这里要将浅层特征和每一个LSRAG做一个加权相连,表示为:
对于RL-NL模块,这里需要说明全局的non-local计算量非常大,而且low level问题喜欢局部的non local。所以这里做区域的non local,通过将特征分解成多个区域操作实现,每一个区域分别进行处理。对于LSRAG模块,这里每一个LSRAG模块都是由若干个残差模块组成的,最后特别的,其会将模块的输入加权处理和最后的特征相加作为最终的输出,如下所示:
这里要特别说明SOCA模块,考虑二阶特征相关性,这里对于一个大小为WHC维的特征,表示为X,其协方差矩阵可以表示为:
协方差的正则化对于表示特征非常重要,所以这里要对协方差矩阵做正则化,其是一个对称的半正定矩阵,可以做特征值分解表示为:
这里U是一个正交矩阵,$\Phi$是一个对角矩阵,值是特征值,以非递增的序列排列。所以协方差正则化表示为:
所以当$\alpha = 1$时,没有正则化,当$\alpha < 1$时,非线性的收缩特征值小于1的部分和拉伸大于1的部分,其中$\alpha=0.5$对于所有的特征表达都有好处,这里使用这个值。最终,通道特征的统计值可以通过$\hat{Y}$的收缩得到,$\hat{Y} = [y_1,….,y_c]$,统计值z的第c维可以表示为:
这里$H_{GCP}$表示为全局协方差池化,和经常使用的一阶池化相比,这里这里池化分析了更高的特征的分布和特征统计量。后面是将上述结果通过两个全连接层获得权重,并且实现channel attention。计算协方差正则化需要大量的计算量,论文提供了一个快速计算方法,具体不表。