这篇论文感觉是一篇讲story的论文,花式连线。借鉴了常微分方程的思想,去设计SR的模块,这个思想在分类里已经有了不错的表现(又是借鉴别人的东西)。目前的超分辨网络有两个缺点,一个是太深了,还有一个是太深训练需要太多trick。论文首先将欧拉方法和残差模块进行比较,说明可以使用ODE方法,然后针对ODE方法设计不同的两种模块,以及G模块的影响。
从动态角度来看,CNN实际上是学习一个输入状态到输出的映射,不同层的状态是可以选择的,如果问题足够平滑,ODE可以产生这样的映射。一般的常微分方程ODE表示如下:
CNN解决SR问题就是以上面公式为基础动态解方程的一个问题,当然直接求解上面的方程比较困难,这里以需要进行近似的数值计算,利用欧拉方法:
即这里使用间隔为h的宽度去近似y’:$y_{n+1} - y_n = hy’$,残差模块类似于如下形式:
即,$G(y_n)=hf(x_n,y_n)$
进行上述步骤迭代可能需要很多步,增加步数或者优化每步都可以达到目标,对应于增加block的数量或者使用更好的模块,当然上述近似只是一阶近似,更好的近似可以达到更好的效果。如果使用蛙跳二阶结构,可以将下面三个公式融合为一个模块:
当然这里G也不需要一定要定义成卷积加relu的形式,只要非线性就行了。还可以用二阶龙格-库塔公式去实现,可以表示为如下形式,具体推导见论文:
和resnet相比,这里的分支更多了,对于三阶龙格-库塔公式,这里表示为:
三种模块的表达如下所示:
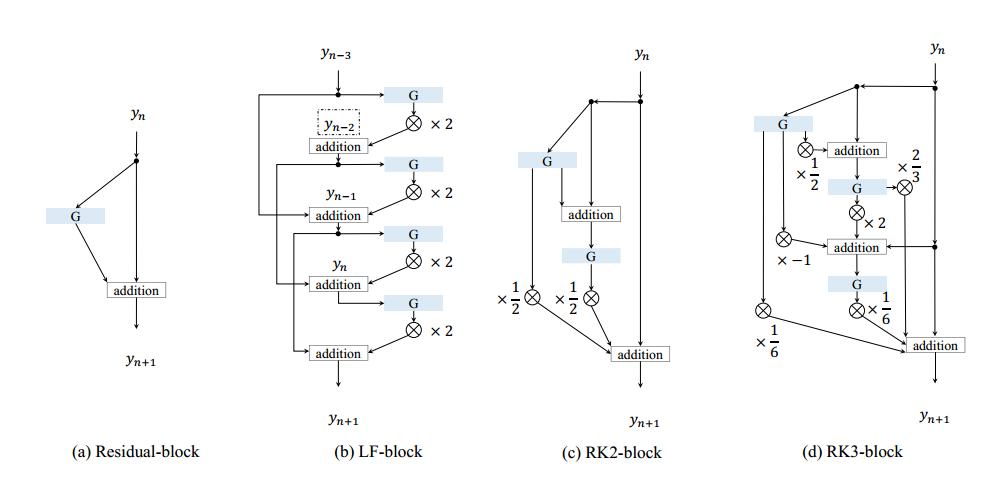
更高阶的表达公式也是更复杂的,G被定义为两个变量之间的函数,其中y是特征图,x是G在网络中的位置。输入和输出特征图在G是不改变的,从而构成ODE和CNN的联系(没看懂这个地方想说啥)。论文使用的整体结构如下所示:
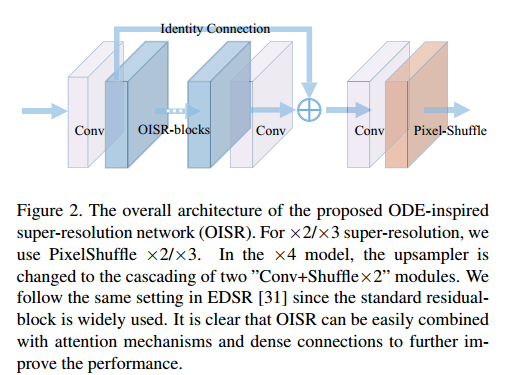
这里步长$h_n$是通过可学习的参量$\alpha$来实现的,这里对其初始化比较重要,一般比较小。G的组成模块一般有如下几种形式,都是非线性的:
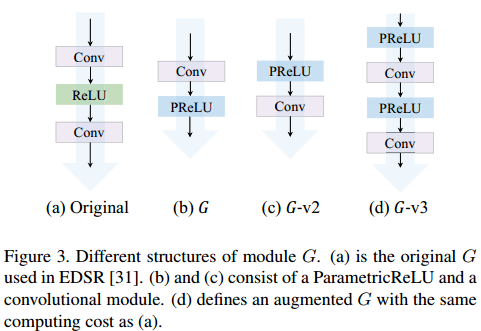
在不同的阶次方法或使用不同的G,这里都是保证参数量是相近的,从而方便比较性能。看了论文提供的表格,PSNR涨幅很有限,其余部分看论文吧。