这篇论文主要是将引导滤波的思想引入到了网络之中,先在小图上进行学习,再通过在引导滤波器上学习针对特定任务的引导图实现对生成小图上采样,最后恢复大图。这种思想在Deep bilateral里面已经使用过,但是这篇论文里生成的大量仿射系数使得速度受到了限制。
Guided Filtering Layer
先看一下引导滤波层,令输入高分辨图为$I_h$,低分辨图为$I_l$,输出的低分辨图为$O_l$,高分辨图为$O_h$,那么在引导滤波里学习的线性变换系数分别令为$A_l$和$b_l$,通过最小化输入和输出的损失可以计算得到这些系数,则有:
其中i是像素的标号,k是引导滤波里局部窗口的标号。$A_h$和$b_h$是$A_l$和$b_l$上采样得到的,这样输出的高分辨图也可以通过线性公式获得,如下所示:
下面到正式的引导滤波层,如下图所示,$A_l$和$b_l$通过一个均值滤波器$f_u$和局部线性模型$I_l$和$O_l$得到,然后通过上采样获得$A_h$和$b_h$。然后线性组会$A_h$和$b_h$以及$I_h$得到输出$O_h$。因此,O_h可以通过反向传播到$A_h$和$b_h$以及$I_h$,进而可以通过引导滤波层直接训练得到$O_l$的网络。
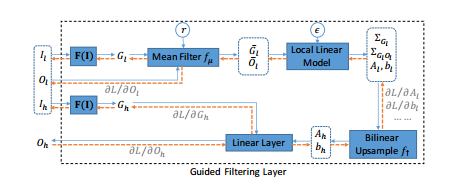
上图中蓝色线代表前向,黄色线代表后向,令r为均值滤波的半径设为0.1,$\epsilon$为正则化系数设为1e-8,算法流程图如下所示:

上图中的算法3,4步和引导滤波求解a,b公式对比,发现几乎完全一样。
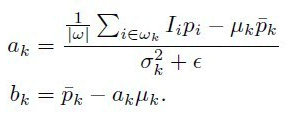
其中,$Ol$和$\overline{O_l}$对应$p$,$\overline{p}$,$\overline{G_l}$、$\Sigma{G_l}$对应于$\mu$,$\sigma^2$。
最后在引导层里引入了F(I),实现层中的转换(如上图所示),其由两层组成,可以根据不同的任务训练得到不同的效果。
Deep Guided Filtering Network
将上述部分和前面学习低分辨的网络部分结合在一起,称为DGF,结构图如下图所示:
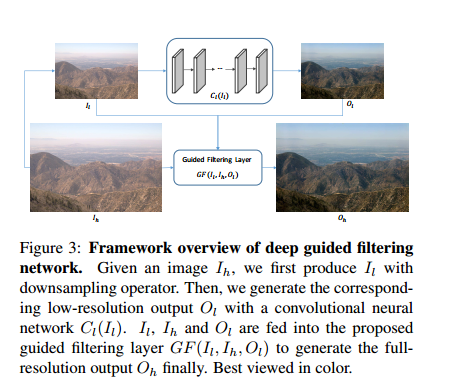
其中前面提取低分辨特征的网络使用的是CAN。首先将原始的引导滤波上采样称为DGFs,其不可训练。然后引入上面提到的引导滤波层,这里的的F(I)都是一个恒等变换函数,称为DGFb。最后,导入上面提出的两层F(I),称为DGF。在图像处理的训练里,将损失函数定义为L2 loss。训练中,其为了获得更好的泛化性能,使用了512s到1672s大小不等的图片作为训练集。而下采样后统一变成64s大小。
实验结果
在运行速度和内存使用上和deep bialteral以及CAN的对比如下图所示:

在不同任务上的效果对比如下所示:
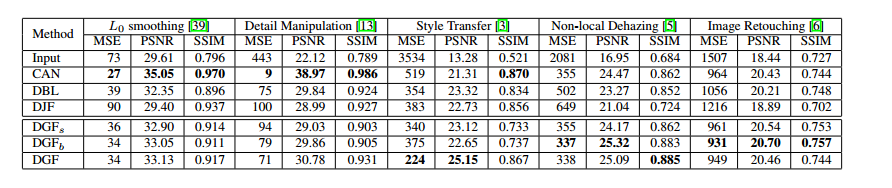
可以看出有些任务上表现不好,这说明这类任务不适合在低分辨下进行处理。此外有些任务在DGF上表现更好,说明这些任务是依赖分辨率的。此外,结果也说明使用不同分辨大小图片作为输入会取得更好的效果,这里不再赘述。