正态分布随机数数目对均值和方差的影响

发表于 | 更新于: | 分类于 | 阅读次数: |
字数统计: 396字 | 阅读时长 ≈ 2分钟

题目描述如下:

首先需要产生数目为num的随机数，均值为mean,方差为sigma的平方，模块如下:

1
2
3
4
5
6
import numpy as np
import matplotlib.pyplot as plt

def StructNumber(mean,sigma,num):
    number = np.random.normal(mean,sigma,num)
    return number

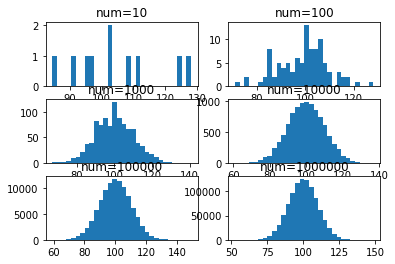
然后本人的思路是，让随机数数目从10依次增加到1000000，设定x和y分别将每次使用新的随机数得到的均值和方差收入其中，方便后面画图。同时在循环里使用直方图，观察它们均值和方差的分布。
结果如下面所示，可以看出随着数据的增加，其均值和方差结果越来越接近100，直方图也显示它们的分布是越来越集中的。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
i = 1
x = []
y = []
t = 1
while i<100001:
    num = i*10
    print(num)
    s = StructNumber(100,10,num)
    i = i*10
    plt.subplot(3,2,t)
    plt.hist(s,30)
    plt.title('num='+str(num))
    mean = s.mean()
    variance = (s*s).sum()/num - mean**2
    print("mean:%.8f,variance:%.8f"%(mean,variance))
    x.append(mean)
    y.append(variance)
    t+=1
plt.show()
10
mean:104.51838985,variance:176.01656876
100
mean:99.18883640,variance:102.91075335
1000
mean:100.14176364,variance:104.66360100
10000
mean:100.01272179,variance:100.81413882
100000
mean:100.05060346,variance:101.20949827
1000000
mean:100.00862825,variance:100.10280875

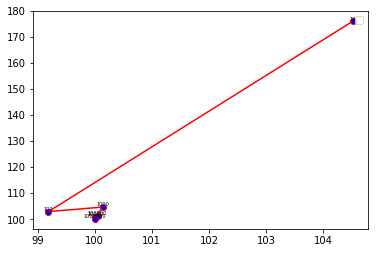
下面用折线图也反映，随着迭代次数的增加，结果收敛于理论值。

1
2
3
4
5
6
7
8
plt.plot(x, y,  color='r',markerfacecolor='blue',marker='o')
num = 1
for a, b in zip(x, y):
    num = num*10
    plt.text(a, b, (num), ha='center', va='bottom', fontsize=5)

plt.legend()
plt.show()
No handlers could be found for logger "matplotlib.legend"
0%