岭回归

发表于 | 更新于: | 分类于 | 阅读次数: |
字数统计: 689字 | 阅读时长 ≈ 3分钟

题目具体要求如下:

这道题有两种方法，第一种是使用sklearn调包求解权重系数，第二种是直接使用公式代入基函数求解。产生y的代码如下所示:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
import numpy as np
import math
import matplotlib.pyplot as plt
from sklearn.linear_model import Ridge


def generate():
    y = []
    x = []
    base= 0.041
    e = np.random.normal(0, 0.3, 25)
    for i in range(25):
        x.append(i*base)
        y.append(math.sin(2*math.pi*x[i]))
    Y = y
    y = y+e
    return x,y,Y

然后是求解权重系数，使用公式直接求解代码如下，其中公式为$(X^T X+\lambda I)^{-1}X^T y$,注意掉注释的部分，是为方法2。

1
2
3
4
5
6
7
8
9
10
11
12
13
def coffecient(lamda):
    x,y,Y = generate()
    X = np.zeros(shape=[25,8])
    for i in range(25):
        for j in range(8):
           X[i,j] = x[i]**j
    XT = X.T
    I = np.eye(8)
    coef = np.dot(np.dot((np.matrix(np.dot(XT,X)+lamda*I)).I,XT),y)
    # clf = Ridge(lamda,fit_intercept=False)
    # clf.fit(X,y)
    # coef = clf.coef_
    return coef,X,x

然后就是求解多项式系数的曲线及其均值，总共是100组数据，每次都产生不同的系数，代码如下:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
def select(lamda):
#     plt.figure()
    y_sum = np.zeros(shape=[25])
    for i in range(100):
        y_data = []
        coef,X,x = coffecient(lamda)
        for i in range(25):
           y = 0
           for j in range(8):
               y = y+coef[0,j]*(X[i,j])
           y_data.append(y)
        y_sum = y_sum+y_data
        y_mean = y_sum / 100
#         plt.plot(x,y_data,color = 'r')
    return x,y_mean

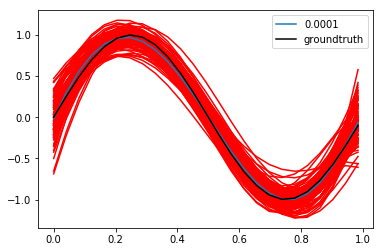
我们取lamda为0.0001，画出100个多项式的曲线及其平均值，以及目标曲线y=sin(2pix)的曲线，如下所示，其中蓝色为平均值曲线，黑色为groundtruth,红色为100个多项式曲线。

1
2
3
4
5
6
7
8
plt.figure()
lamda = 0.0001
x, y_mean = select(lamda)
plt.plot(x, y_mean, label=lamda)
x,y,Y = generate()
plt.plot(x,Y,label = 'groundtruth',color='black')
plt.legend()
plt.show()
<matplotlib.figure.Figure at 0x7f4ac450e910>

然后我们让lamda从0.001依次x10变到1，观察各lamda对应的多项式平均值变化趋势，次步先将上面的select里的plot注释，再执行下面代码，防止多个多项式的干扰，结果如下所示:

1
2
3
4
5
6
7
8
9
10
plt.figure()
for lamda in 0.001,0.01,0.1,1:
    x,y_mean = select(lamda)
    plt.plot(x,y_mean,label = lamda)
plt.xlabel('x')
plt.ylabel('y')
x,y,Y = generate()
plt.plot(x,Y,label = 'groundtruth',color='black')
plt.legend()
plt.show()

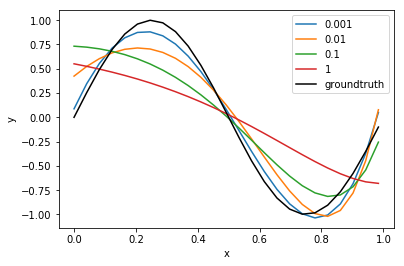
可以看出,lamda的值越小，其距离真实值的偏差越小，符合我们在课上学习得到的偏差，方差中对lamda作用的理解。
此外，将def coffecient(lamda):里注释的三行注释删去，同时去除上面的一行代码，是使用sklearn进行求解，图与上面一样，这里不再赘述。

0%