实现朴素贝叶斯

发表于 | 更新于: | 分类于 | 阅读次数: |
字数统计: 659字 | 阅读时长 ≈ 3分钟

题目要求如下：

2018-11-21 13-35-11屏幕截图.png

2018-11-21 13-35-27屏幕截图.png

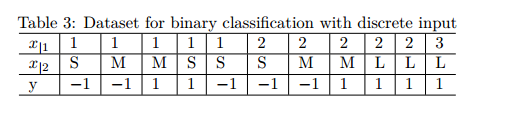
和上次作业一样，这里我们令S=1，M=2，L=3，对该题进行求解：

首先还是产生数据，如下所示：

1
2
3
4
5
6
7
import numpy as np

def produce_sample():
    x1 = np.array([1,1,1,1,1,2,2,2,2,2,3])
    x2 = np.array([1,2,2,1,1,1,2,2,3,3,3])
    y = np.array([-1,-1,1,1,-1,-1,-1,1,1,1,1])
    return x1,x2,y

然后统计一个属性的类别个数以及种类数，如下所示：

1
2
3
4
5
6
7
8
9
10
11
12
def all_np(arr):
    arr = np.array(arr)
    key = np.unique(arr)
    result = []
    count = 0
    for k in key:
        mask = (arr == k)
        arr_new = arr[mask]
        v = arr_new.size
        result.append([k,v])
        count+=1
    return np.array(result),count

然后就是统计一个属性里各个类别和标签之间各自对应的个数，注意这里的np.logical_and检查两个数组里都为真的部分，为关键判别部分：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
def cal_xy(x,y):
    arr = np.array(x)
    key_x = np.unique(x)
    key_y = np.unique(y)
    result = []
    for k_y in key_y:
        for k_x in key_x:
            mask_x = (x == k_x)
            mask_y = (y == k_y)
            mask = np.logical_and(mask_x,mask_y)
            arr_new = arr[mask]
            v = arr_new.size
            result.append([k_x,k_y,v])
    return np.array(result)

然后就是朴素贝叶斯的计算，这里将所有属性和类别的概率（先验和条件概率）都计算出来，然后计算它们所对应的似然概率，并且保存返回，作为后面判别的依据：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
def NaiveBaiyes(alpha):
    x1,x2,y = produce_sample()
    y_list,count_y = all_np(y)
    x1_list,count_x1 = all_np(x1)
    x2_list,count_x2 = all_np(x2)
    y_prob = (y_list[:,1]+alpha*1)/(y.size+alpha*count_y)

    probx1_y = cal_xy(x1,y)[:,-1]
    probx1_y0 = (probx1_y[:3]+alpha*1)/(y_list[:,1][0]+alpha*count_x1)
    probx1_y1 = (probx1_y[3:] + alpha * 1) / (y_list[:, 1][1] + alpha * count_x1)

    probx2_y = cal_xy(x2,y)[:,-1]
    probx2_y0 = (probx2_y[:3]+alpha*1)/(y_list[:,1][0]+alpha*count_x2)
    probx2_y1 = (probx2_y[3:] + alpha * 1) / (y_list[:, 1][1] + alpha * count_x2)

    return y_prob,probx1_y0,probx1_y1,probx2_y0,probx2_y1

最后是对输入的数据进行判别，判别类别似然概率较大的那一组就被认定为所要判定成的类别：

1
2
3
4
5
6
7
8
9
10
11
def check(x,y,alpha):
    y_prob, probx1_y0, probx1_y1, probx2_y0, probx2_y1 = NaiveBaiyes(alpha)
    x1_label = x-1
    x2_label = y-1
    yjunw_pre0 = y_prob[0]*probx1_y0[x1_label]*probx2_y0[x2_label]
    y_pre1 = y_prob[1]*probx1_y1[x1_label]*probx2_y1[x2_label]
    if y_pre0>y_pre1:
        print("The label is -1")
    else:
        print("The label is 1")
    print("prediction of -1 is %.4f,prediction 1 is %.4f"%(y_pre0,y_pre1))

最后进行判别，输入数据（1，M)对应（1，2）,当alpha为0时，结果如下：

1
check(1,2,alpha=0)
The label is -1
prediction of -1 is 0.1091,prediction 1 is 0.0606

当alpha结果为1时，结果如下：

1
check(1,2,alpha=1)
The label is -1
prediction of -1 is 0.0865,prediction 1 is 0.0598

1
可以看出最后判别的结果均为-1。
0%